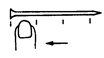【補充】：

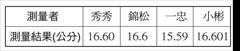
(一) 測量結果的表示：

A、 『今天的天氣好熱！』，『那個人好高！』，此種敘述稱為【定性】的敘述。

B、 實驗過程中，我們將觀察結果給與【數量】化的程序，成為【定量】的敘述。

C、 測量結果含【數字】及【單位】兩部分。

D、 測量時需採用特定的【標準量】和【待測物】比較，我們稱此標準量為【單位】。
測量結果得到標準量的整數倍，此倍數即為【數字】部分。

E、 測量相同的物理量時，數字部分不一定相同，這是由於：

(1) 使用的【最小刻度】不同。

(2) 【儀器】不同。

(3) 【操作】不當。

F、 任何測量的結果免不了要進行【估計】，因此必然會產生【誤差】。

G、 可以【直接數出來的】不需估計。

例：人數､個數､天數､年齡、日期等。

(A) 全班學生45人。《人數》 (B) 桌上有西瓜12個。《個數》

(C) 班長今年14歲。《年齡》 (D) 一天有24小時。 《日期》

(二) 單位的選擇：

A、 符合公認、合理、好用的原則。 例：公分､公釐､公尺､公里､呎､碼。

註：目前世界各國公認的單位系統為【公制】單位。

B、 可選擇適當的單位，避免產生太大的誤差。

例：筆長､掌距､掌寬､公分､公釐､一箭之遙。

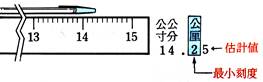
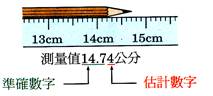
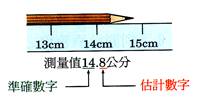
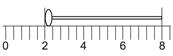
C、 測量值 ＝【準確值】＋【一】位【估計值】。

D、 最小刻度：【準確值】的倒數第【一】位為最小刻度，

或是【測量值】的倒數第【二】位為最小刻度。

(三) 誤差：

A、 誤差的原因：

1. 每人【估計】不同；

2. 【測量儀器】不精確；

3. 【測量方法】不正確。

B、 減少誤差的方法：

1. 使用【較小的刻度】；

2. 進行【多次測量】；

3. 同時【多人測量】；

4. 一次【多量測量】；再求【平均值】。

C、 平均值＝測量結果總和 ÷ 測量次數。

【註】：誤差太大的測量值應捨棄。

D、 注意事項：

1. 使用刻度愈小，測量結果愈準確，誤差愈小。

2. 測量次數愈多，其平均值愈準確，誤差愈小。

3. 求平均值前先將明顯誤差的數值先刪除。

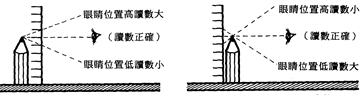
(一) 測量的技巧

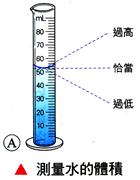
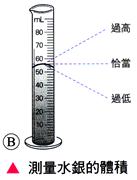
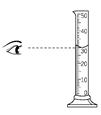
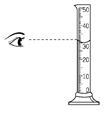
A、 測量者的位置：

B、 量筒的測量：

(1) 測量水的體積	(2) 測量水銀的體積
(1)量筒內裝水，由於水的內聚力小於水與玻璃間的附著力，因此兩邊的水位較高，中央的水位較低，因此形成凹面。 (2)測量時，觀察中央最低點，且視線與量筒的刻度面垂直。 (3)測量的結果，測量值＜實際值。	(1)量筒內裝水銀，由於水銀內聚力大於水銀與玻璃間的附著力，因此兩邊的液面較低，中央的液面較高，因此形成凸面。 (2)測量時，觀察中央最高點，且視線與量筒的刻度面垂直。 (3)測量的結果，測量值＞實際值。

例1. 下列各敘述中，那些是測量結果，是的請打『ˇ』?
(1)阿花的身高__ˇ__ (4)脈膊每分鐘跳動的次數__ˇ__ (7)家裡每月的收入_____
(2)阿達今年13歲____ (5)汽車的行車里程數__ˇ__ (8)台北市的面積___ˇ____
(3)一天有1440分____ (6)馬路上有15棵樹______ (9)一支原子筆7元______

【答案】：(1)(4)(5)(8)

【解析】：(1) 身高(測量長度)；每分鐘的脈搏(測量時間)；
行駛的里程數(測量長度)；台北市的面積(測量長度)。
(2) 年齡不用測量；一天的時間是規定；15棵樹直接數；
金錢收入、買賣金額不用測量，不能有誤差。

例2. 下列那些測量的結果會產生誤差?
(1)今天的氣溫_ˇ__ (2)每月用電量_ˇ_ (3)曉東的血壓_ˇ__ (4)郵局的存款____
(5)王菲的體重_ˇ__ (6)市長的選票____ (7)考試的成績____ (8)胡瓜的身高__ˇ__

【答案】：(1)(2)(3)(5)(8)

【解析】：(1) 氣溫(用溫度計測量)、電量(用瓦時計電表測量)、血壓(用血壓計測量)、
體重(用磅秤測量)、身高(用尺測量)。
(2) 存款、選票、成績不能有誤差，不需要測量。

例3. 下列各測量結果的最小刻度各是什麼？

(1) 3.692 m的最小刻度為________ (5) 42.3952公引的最小刻度為_____

(2) 562.395 km的最小刻度為_____ (6) 38.95384 km的最小刻度為______

(3) 3.846×10⁴ cm的最小刻度為____ (7) 3.6986×10² cm的最小刻度為_____

(4) 6.32×10^-2 km的最小刻度為_____ (8) 4682.6543 km的最小刻度為_____

【答案】： (1) 公分 (2) 公丈 (3) 公尺 (4) 公尺
(5) 公寸 (6) 公寸 (7) 公釐 (8) 公尺

【解析】：原則：個位數為表示的單位，向後數至倒數第二位數字。
(1) 3.692 m  3(公尺).6(公寸)9(公分)2
(2) 562.395 km  562(公里).3(公引)9(公丈)5
(3) 3.846×10⁴ cm  3.846×10⁴ cm 數到4  將科學記號展開 38460 cm
 384(公尺)6(公寸)0(公分)
(4) 6.32×10^-2 km  數到3 將科學記號展開 0.0632 km
 0(公里).0(公引)6(公丈)3(公尺)2
(5) 42.3952公引  42(公引).3(公丈)9(公尺)5(公寸)2
(6) 38.95384 km  38(公里).9(公引)5(公丈)3(公尺)8(公寸)4
(7) 3.6986×10² cm  數到8 將科學記號展開 369.86 cm
 369(公分).8(公釐)6
(8) 4682.6543 km  4682(公里).6(公引)5(公丈)4(公尺)3

例4. 下列的測量值請標示出何者為準確值？何者為估計值？

測量值	準確值	估計值	最小刻度	測量值	準確值	估計值	最小刻度
3.854km	3.85km	0.004km	公丈	0.092kg	0.09kg	0.002kg	0.01kg
35.47m	35.4m	0.07m	公寸	5.555g	5.55g	0.005g	0.01g
0.352cm	0.35cm	0.002cm	0.1公釐	25.32℃	25.3℃	0.02℃	0.1℃

【答案】：如上表

【解析】：測量值＝準確值＋一位估計值
(1) 3.854km ＝ 3.85km(準確值)＋0.04km(估計值)
準確值3.85km  最小刻度 3(公里).8(公引)5(公丈)
(2) 35.47m ＝ 35.4m(準確值)＋0.07m(估計值)
準確值 35.4 m  最小刻度 35(公尺).4(公寸)
(3) 0.352 cm ＝ 0.35cm(準確值) ＋ 0.02cm(估計值)
準確值 0.35cm  最小刻度 0(公分).3(公釐)5(0.1公釐)
(4) 0.092 kg ＝ 0.09kg(準確值) ＋ 0.02kg(估計值)
準確值 0.09kg  最小刻度 0(kg).0(0.1kg)9(0.01kg)
(5) 5.555g ＝ 5.55g(準確值)＋0.005g(估計值)
準確值 5.55g  最小刻度 5(g).5(0.1g)5(0.01g)
(6) 25.32 ℃ ＝ 25.3℃(準確值)＋0.02℃(估計值)
準確值 25.3 ℃  最小刻度25(℃).3(0.1℃)

例5. A、B、C三物體分別以直尺測量其長度，試根據下圖回答問題(圖中數字單位為公分)

(1) A的長度寫成_______公分。

測量值(公分)	2.29	2.30	2.31	2.32	2.33
人數(人)	4	8	12	9	7

(2) B的長度下列何者正確? (A)4公分 (B)4.0公分 (C)4.00公分 (D)4.000公分。_____。

(3) 物體C由全班一起測量，其結果如上表，則C的平均值為_______公分。

【答案】：(1) 6.0cm (2) 4.00cm (3) 2.31cm

測量值(公分)	2.29	2.30	2.31	2.32	2.33
平移數值	-0.01	0	0.01	0.02	0.03
人數(人)	4	8	12	9	7

【解析】：(1) A的長度為6 cm，考慮最小刻度為cm及估計值為 mm，
A應表示為 6.0 cm
(2) B的長度為 4 cm，
考慮最小刻度為mm，估計值應為0.1mm，
B應表示為 4.00 cm
(3) 以2.30為基準，將數值平移，
(－0.01×4＋0×8＋0.01×12＋0.02×9＋0.03×7) ÷ 40 ＝0.011
 平均值為 2.30＋0.011＝2.311
 考慮最小刻度應表示為 2.31 cm

例6. 某生欲測量沙的體積，做下列實驗：

(1) 把乾燥的沙裝入量筒內，輕敲量筒，此時沙面刻度為235cm³。

(2) 用另一量筒取100cm³的水，倒入盛沙的量筒內，發現沙面降到190cm³，水面則指示215cm³。
根據上述的實驗，試回答下列問題：

(1) 倒入100cm³的水，但沙面上的水只有25cm³，這是因為 (A)沙溶於水 (B)水溶於沙 (C)水浸入沙粒的空隙內的關係。_______。

(2) 沙粒的體積有 (A)190cm³ (B)115cm³ (C)135cm³ (D)75cm³。_______。

(3) 本實驗是利用沙的何種性質？__________________________________。

【答案】：(1) C (2) B (3) 砂不溶於水且沉於水中

【解析】：(1) 倒入100cm³的水，但是砂面上只有25cm³，因部分的水滲入沙中的空隙。
(2) 最高水面刻度(215cm³)＝砂的體積＋加入水的體積(100cm³)
 砂的體積＝215－100＝115cm³
(3) 糖不能以此方法測量，因糖能溶於水；
木塊不能以此方法測量，因木塊能能沉於水中。
砂不溶於水，且沉於水中，因此：
將全部的總體積(水面的刻度)－最初水的體積，即為砂的體積。

例7. 某圓柱形容器容積為450立方公分，裝300立方公分水後，液面高度為10公分，則：

(1) 此容器的底面積為________平方公分；

(2) 放入木塊後發現溢出60c.c，且木塊露出70公分³於水面上，則木塊體積_____cm³。

【答案】：(1) 30 cm² (2) 280 cm³

【解析】：(1) 容器的容積＝底面積×高  300＝ A × 10  底面積 A＝30 cm²
(2) 木塊會浮於水面，木塊的體積＝沉入水中的體積＋露出液面的體積
沉入水中的體積＝液面上升的體積＋溢出容器的體積
＝(450－300)＋60＝150＋60＝210cm3
木塊總體積＝210＋70＝280 cm³

例8. 有一量筒內裝有600ml的水，其水深20cm。今投入一木塊於量筒內，木塊浮於水面而靜止，水位上升至22cm;若木塊下端繫一塊鐵塊，僅鐵塊沈入水中時，水位上升至23cm；當鐵塊與木塊一起沈入水中時，水位上升至27cm，則:

(1) 量筒底面積為______。

(2) 鐵塊體積為______。

(3) 木塊體積為______。

【答案】：(1) 30cm² (2) 90 cm³ (3) 120cm³

【解析】：(1) 底面積×高＝體積  A×20＝600  A＝30 cm²
(2) 投入鐵塊時，液面由 20cm 上升至23cm  鐵塊使液面升高3cm
 鐵塊的體積＝液體升高的體積＝底面積×高＝30×3＝90cm³
(3) 投入木塊＋鐵塊後，全部沉入水中的體積＝液面升高的體積
 液面由20cm 上升至27cm，表示全部上升7 cm
 鐵塊使液面上升3cm，木塊使液面上升4cm
 木塊體積＝30×4＝120cm³

例9. 量筒底面積100cm²，高40cm，裝35cm的水，今投入體積2000cm³的金屬球後，溢出量筒的體積為_______cm³。

【答案】：1500cm³

【解析】：金屬球會完全沒入水中，金屬球的體積＝水面上升的體積＋溢出量筒的體積
金屬球投入後，液面由35cm上升至40cm，隨後溢出，
2000＝100×(40－35)＋V＝100×5＋V＝500＋V  V＝2000－500＝1500cm³

例10.有大小兩量筒，底面直徑比為6：1，今將一定量的水倒入小量筒中，若水深為54cm，改倒入大量筒中時，水面的高度應為_______cm。

【答案】：1.5cm

【解析】：底面積比＝直徑的平方比  底面積比 A₁：A₂＝6²：1²＝36：1
水倒入大量筒與小量筒的體積相同，液體體積＝底面積 × 液體上升高度
36× h₁＝1×h₂  36×H₁＝1×54  H₁＝54÷36＝1.5 cm

例11.底面積100cm²、高30cm的圓筒，裝水20cm深，放入一木塊後，水面上升4cm，且木塊浮於水面上，在木塊底下綁150cm³的鐵塊後再沉入水中，則水面再升高6公分，此木塊體積為________cm³。

【答案】：850 cm³

【解析】：木塊和鐵塊投入水中，共上升了4cm+6cm＝10cm
上升的體積＝ 底面積 × 高 ＝ 木塊的體積＋鐵塊的體積
100×10 ＝ V＋150  V＝1000－150＝850 cm³

例12.若地圖上的比例尺為1：1000，則：

(1) 地圖上1cm實際長______cm，或________m；

(2) 地圖上5cm實際長______cm，或________m；

(3) 地圖上1cm²實際面積________m²。

(4) 地圖上4cm²實際面積________m²。

【答案】：(1) 1000，10 (2) 5000，50 (3) 100 (4) 400

【解析】：(1) 比例尺1：1000 地圖上1cm，實際長度為1000 cm，即為10 m
(2) 地圖上5 cm，實際長度為5000 cm，相當於50 m
(3) 地圖上1cm，實際長度為10m
 地圖上 1cm²，實際面積為 (10 m)²＝100 m²
(4) 地圖上4cm²，實際面積為 100×4＝400 m²

例13.右圖是某區之部分地圖其比例尺是1:10000，則：

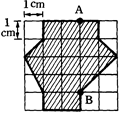
(1) 如右圖，斜線面積為______小方格。

(2) 斜線面積是______cm²。

(3) 圖上1公分所代表實際長度是 (A)10000公尺 (B)1000公尺 (C)100公尺 (D)1公尺。______。

(4) 圖上AB間所代表實際長度是______公尺。

(5) 圖上斜線部分所代表實際面積是______m²；相當於______km²。

【答案】：(1) 16.0 (2) 16.0 (3) C (4) 400 (5) 1.6×10⁵ m²、1.6×10^－1

【解析】：完整的視為1格，不完整的當成半格(0.5格)
(1) 如圖，完整的有13格，不完整的有 6格，
總面積＝13格＋ 6×0.5＝13＋3.0＝16.0格
(2) 1小格＝ 1cm×1cm＝1 cm² ，圖中共有16.0小格，
地圖上的面積為 16.0 × 1 ＝ 16.0 cm²
(3) 比例尺為 1：10000，即地圖上1cm，實際長度為 10000cm，相當於 100 m
(4) AB間共4 cm長，因此實際長度為 100×4＝400 m
(5) 地圖上1cm，實際長度為 10000cm，相當於 100 m
 地圖上 1 cm²，實際面積為 (100m)²＝10000 m²＝10⁴ m² ＝10^－2 km²
 16.0 × 10⁴ ＝ 1.6 ×10⁵ m² ＝ 1.6×10^－1 km²

例14.一不規則圖形其面積未知，我們用均勻厚薄的紙片，剪出與此面積同大小的圖形，若每一小方格面積4cm²，質量0.2克，若測出此不規則圖形質量為4.7克，則：

(1) 此不規則圖形約_______小方格。

(2) 此不規則圖形面積約為_______cm²。

【答案】：(1) 23.5 (2) 94

【解析】：面積愈大，所秤得的質量愈大，因此面積比＝質量比
1小格質量0.2g，總面積共4.7g，相當於 4.7÷0.2＝23.5小格
4cm²：0.2g ＝ A：4.7g è  A＝

例15.如圖，小華測量櫻花湖的平面圖，請回答下列問題：

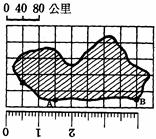
(1) 以尺測量AB長度，應記為_____cm。(尺面數字代表公分)

(2) 以小方格為單位，此圖的面積約為______小方格。(不足一格者皆以0.5格計算)

(3) 櫻花湖的實際面積應為_______km²。

(4) 若將此平面圖剪下，以天秤測量5次，結果如下：33.8克、33.7克、33.6克、33.4克、38.3克。則此圖形測得的質量應記為______克。

(5) 承上題，已知每一方格質量1.4克，由前題推算此土地的實際面積應為_______km²。

(6) 若實驗過程力求精確，則以上兩種測量面積的方法，Ａ以方格紙估計；Ｂ剪下圖形以天平測量質量那一種的誤差比較小。_________。

【答案】：(1) 2.50 (2) 23.0 (3) 36800 (4) 33.6 (5) 38400 (6) B

【解析】：(1) AB間長度共5小格長，1小格長度 5mm，
AB長為 5×5＝25.0 mm(記得加估計值)，相當於 2.50cm
(2) 如圖，完整的有10格，不完整的有 26格
圖形面積＝10＋ 26×0.5＝10＋13.0＝23.0小格
(3) 1小格長度40km，1小格面積＝(40km)²＝1600 km²
23.0 × 1600 ＝ 36800 km²
(4) 平均值＝(33.8＋33.7＋33.6＋33.4)÷4＝33.625 g
考慮最小刻度，表示成 33.6 g，(38.3g與其他測量值的誤差太大，直接捨去)
(5) 1.4g：1600km²＝33.6：A  A＝38400 km²
(6) 以天平測量值量，再換算成面積，所得到的誤差較小。

( )1. 有關「我家學校」距離的測量，下列何者較易取得大家的同意?
(A)騎腳踏車約600轉 (B)坐公車約30分鐘 (C)坐計程車共需45元 (D)兩地步行約2.5公里。

【答案】：(D)

【解析】：以供認的長度為單位，較容易為大家接受且能理解距離為多少。

( )2. 某物體的長度測量結果記錄為5.678公尺，亦可記為567.8公分，二者的
(A)單位相同，數字不同 (B)單位不同，數字相同 (C)單位、數字均相同 (D)單位、數字均不同。

【答案】：(D)

【解析】：比較兩者，5.678與567.8不同，公尺與公分不同，因此兩者的測量結果，單位不同、數字不同。

( )3. 下列那一種是由測量結果所得?
(A)今天下午的氣溫是25℃ (B)班長的口令聲音很大 (C)這個西瓜很好吃 (D)今天下午下了很大的雨。

【答案】：(A)

【解析】：以儀器測量需要估計，氣溫需使用溫度計，並且測量結果有準確值、估計值，測量結果有誤差產生。

( )4. 下列那一項是測量的結果?
(A)全校學生共3520人 (B)鐘擺擺動一次需1秒 (C)一星期有7天 (D)一張方格紙有小方格2400個。

【答案】：(B)

【解析】：時間的長短需要以馬錶或計時器測量，側有誤差產生。

( )5. 下列何者為測量的結果?
(A)2年7班學生人數43人 (B)今天氣溫28℃ (C)理化課本有171頁 (D)註冊費2352元。

【答案】：(B)

【解析】：氣溫為測量的結果。

( )6. 下列那一項沒有誤差?
(A)今天降雨量是13.2公釐 (B)二年級男生有532人 (C)今日氣溫21℃ (D)現在時間是10點30分。

【答案】：(B)

【解析】：人數是直接數，只能有唯一的一個數值，不能有誤差。
降雨量以量雨計測量、氣溫以溫度計測量、時間以手錶測量，會有誤差產生。

( )7. 下列測量結果，那一項不是完整的敘述?
(A)明仁身高120 (B)小英體重30公斤 (C)桌子長度是6.5手掌寬 (D)小明跑百米的時間是心跳20次。

【答案】：(A)

【解析】：完整的測量結果，須包含數字與單位，身高120缺少單位，不是完整的描述。

( )8. 如右圖的鐵釘長度應記為
(A)3手指寬 (B)3.15手指寬 (C)3.2手指寬 (D)3.3公分。

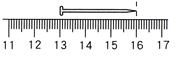
【答案】：(C)

【解析】：如圖，鐵釘長度為3格多一些，因此準確值為3.0手指寬，估計值可表示為0.2手指寬，所以應寫成3.2手指寬。

( )9. 某生使用最小刻度為公釐的直尺測物長，正好是36公分，則最好記作
(A)36公分 (B)36.0公分 (C)36.00公分 (D)36.000公分。

【答案】：(C)

【解析】：最小刻度為公釐(mm)，應將36公分表示為36.00公分。
36(公分).0(公釐，最小刻度)0(估計值)

( )10. 某生以最小刻度為公釐的直尺，量得某輪軸長為15公分，則此測量數字應記為
(A)15公分 (B)15.0公分 (C)15.00公分 (D)15.000公分。

【答案】：(C)

【解析】：最小刻度為公釐，測量長度為15公分，應表示成15.00公分。
15(公分).0(公釐，最小刻度)0(估計值)

( )11. 一直尺最小刻度是公釐，某同學用此直尺量一原子筆的長度，則其測量值的表示法以下列何者為最佳?
(A)13.42公分 (B)13.4210公分 (C)13.421公分 (D)13.42100公分。

【答案】：(A)

【解析】：最小刻度為公釐，則測量值應為13.42公分。
13(公分).4(公釐，最小刻度)2(估計值)

( )12. 一支鉛筆的兩端各恰對準直尺(最小刻度為公分)上的刻度數各為14刻度與26刻度，則此鉛筆的長度為
(A)12.00公分 (B)12.0公分 (C)12公分 (D)以上皆合理。

【答案】：(B)

【解析】：鉛筆兩端的刻度為14、、26，則測量值為26－14＝12公分。
最小刻度為公分，則應表示為12.0公分。
12(公分，最小刻度).0(估計值)

( )13. 某生用最小刻度分別為公寸、公分、公釐之直尺，測得桌長皆為2公尺，測得準確度較大的刻度為
(A)公寸 (B)公分 (C)公釐 (D)一樣準確。

【答案】：(C)

【解析】：測量儀器的最小刻度愈精細，測量結果的誤差將愈小，準確度愈大。

( )14. 以刻度毫米的米尺測量一枚鎳幣厚度，設每枚厚度均相等；則下列那一結果的準確度較高?
(A)直接測量一枚的厚度 (B)測量5枚的總厚度再除以5 (C)測量10枚的總厚度再除以10 (D)測量100枚的總厚度再除以100。

【答案】：(D)

【解析】：減少誤差的方法，可以以多量測量，再求平均值，因此先將鎳幣疊起，測量之後再算平均，測量的數量愈多，所測得的平均值將愈準確，誤差也愈小。

( )15. 下列測量值的記錄，何者錯誤?
(A)書桌的寬度是5.8手掌寬 (B)書桌的長度是10.56手掌寬　 (C)用最小刻度為公分的直尺，測量書桌長90.0公分 　(D)用最小刻度為公釐的直尺，測量鉛筆長度152.5公釐。

【答案】：(B)

【解析】：測量時以手掌寬為最小的測量單位，再加一位估計值；所以表示到小數第一位，因此10.56手掌寬多了一位數值，寫成10.5或10.6個手掌寬即可。

( )16. 某生用一直尺測量某物，其長度為3.2公分，則下列敘述何項正確?
(甲)此物體長度恰為3.2公分 (乙)所用直尺的最小刻度為公分
(丙)所用直尺的最小刻度為公釐 (丁)準確值為3公分，估計值為0.2公分。
(A)甲丙 (B)乙丁 (C)甲乙丙 (D)乙丙丁。

【答案】：(B)

【解析】：測量結果一定有誤差，所得3.2公分，其中準確值為3公分，估計值為0.2公分，
3(公分，最小刻度).2(估計值)，因此最小刻度為公分，

( )17. 下列敘述何者正確?
(A)使用最小刻度為公釐的直尺測得鉛筆長正好是14公分時，應記為14.0公分 (B)最小刻度為公釐的直尺，測得10枚一疊的鎳幣的總厚度，再求出一枚鎳幣的平均厚度可準確到公釐 (C)某生用直尺測得某物的長為1.256公尺，由此數值可知直尺的最小刻度為公分 (D)以上敘述皆不正確。

【答案】：(C)

【解析】：(A) 最小刻度為公釐，應表示成14.00公分，14(公分).0(公釐，最小刻度)0(估計值)
(B) 最小刻度為公釐，測量10枚再求平均，每一個鎳幣可準確到0.1公釐。
(C) 1.256公尺的最小刻度為公分。
1(公尺).2(公寸)5(公分，最小刻度)6

( )18. 某生以直尺測量一木棒長度記錄為2.345×10³ 公釐，則該生所使用的最小刻度為
(A)公尺 (B)公寸 (C)公分 (D)公釐。

【答案】：(C)

【解析】：2.345×10³公釐，最小刻度的數字為4，將科學記號展開為2345公釐，則最小刻度為公分，234(公分，最小刻度)5(公釐，估計值)

( )19. 某生以直尺測量甲、乙、丙三物體，所使用所得的三個測量值分別為甲＝1.201公尺、乙＝58.2公分、丙＝3.425×10²公釐，可知使用直尺之最小刻度
(A)甲與乙相同 (B)乙與丙相同 (C)丙與甲相同 (D)甲乙丙均相同。

【答案】：(A)

【解析】：甲＝1.201公尺，最小刻度為公分，1(公尺).2(公寸)0(公分，最小刻度)1(公釐，估計值)
乙＝58.2公分，最小刻度為公分，58(公分).2(公釐，估計值)。
丙＝3.425×10²公釐，最小刻度的數字為2，將科學記號展開，得到342.5公釐，最小刻度為公釐，342(公釐，最小刻度).5(0.1公釐，估計值)。

( )20. 某人用一直尺測得物長為7.462公尺，再以此直尺測量另一物長，恰為2公尺16公分，則應表示為
(A)2.16公尺 (B)21.60公寸 (C)216.00公分 (D)2160.0公釐。

【答案】：(B)

【解析】：7.462公尺，最小刻度為公分，7(公尺).4(公寸)6(公分，最小刻度)2(公釐，估計值)

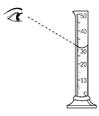
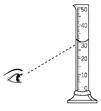
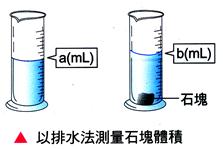
( )21. 量筒內裝水指示出的刻度為40c.c.(ml)，今於量筒內丟入一石塊，則
(A)由液面刻度無法確定石頭的體積 (B)液面將小於40c.c.刻度，石頭的體積等於液面的刻度 (C)液面將高於40c.c.刻度，石頭的體積等於兩液面刻度差 (D)液面保持在40 c.c刻度，石頭的體積須另外測定。

【答案】：(C)

【解析】：將石塊投入量筒中，則石頭沒入水中，液面上升，且上升的體積(後來水位高度－原來水位高度)，等於石頭的體積。
因此原液面高度40cc，石頭投入後，水面超過40cc，，

( )22. 使用有刻度之量筒量取水之體積時，觀察者之視線(如右圖之虛線)應取那一方向，所得之讀數比較合理?
(A)甲 (B)乙 (C)丙 (D)丁。

【答案】：(C)

【解析】：以量筒測量液體的體積時，視線要對準中央的最低點，並且須和刻度面保持垂直，，才能減少誤差。

( )23. 小玉依標準位置測量量筒內水的體積，測量值將比實際值為
(A)大 (B)相等 (C)小 (D)不一定。

【答案】：(C)

【解析】：依標準位置測量量筒中的水，因水面為凹面，因此測量結果小於實際的真正體積。

( )24. 小詩郊遊時，在大樹旁拍一張照片，如圖。她的身高約160公分，由這張照片，估計這顆樹的高度約為
(A)3公尺 (B)5公尺 (C)7公尺 (D)9公尺。

【答案】：(B)

【解析】：以直尺測量樹的高度及人的高度，樹木的高度約4.3公分，人的高度約1.4公分，即數的高度為人的3倍，因此160×3＝480公分，約為5公尺左右。

( )25. 下列的實驗操作何者正確？
(A)測量量筒體積時，需先將量筒置於桌上，再以眼睛對齊液面中央的最低點刻度，以讀取讀數 (B)欲聞藥品氣味，為求確實，應將鼻子直接靠近容器口嗅之 (C)加熱試管時，管口需朝向自己，以便於觀看 (D)以直尺測量物體長度，視線需和尺面平行，才能判斷正確。

【答案】：(A)

【解析】：(A) 為正確的量筒操作方式
(B) 聞藥品氣味，應以手輕搧嗅聞，不可直接以口鼻靠近。
(C) 試管加熱，不可將管口朝向任何人，以避免危險。
(D) 以直尺測量長度，視線須與尺面垂直，才能得到正確的結果。

( )26. 我們測量一把砂子體積， 先將砂子放入量筒中，輕敲量筒使砂子落下，發現砂面刻度為60cm³，倒入50 cm³的水，再輕敲量筒，發現水面高於砂面，且水面刻度為80cm³，則砂子的體積為
(A)50 (B)40 (C)30 (D)20 cm³。

【答案】：(C)

【解析】：最高水面刻度＝水的體積＋砂的體積
80＝50＋砂 砂的體積＝30cm³

( )27. 三個半徑相同的圓柱水壺，如圖。每個水壺最大盛水量間的關係，下列何者正確?
(A)甲＝乙>丙 (B)甲＝乙<丙 (C)甲>乙>丙 (D)甲<乙<丙。

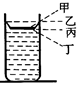
【答案】：(A)

【解析】：壺口的高度，即為壺內的水位高度，如圖，甲＝乙＞丙。

( )28. 在一200毫升的燒杯中，裝盛150毫升的水，今投入一木塊，發現溢出70毫升的水，則木塊的體積為
(A)小於50毫升 (B)50∼70毫升之間 (C)70∼120毫升之間 (D)大於120毫升。

【答案】：(D)

【解析】：木塊投入，水面上升後，隨後液體溢出，
木塊體積＝水面上升的體積＋溢出的液體體積＋木塊露出的體積＝(200－150)＋70＋露出的體積＞120毫升。

( )29. 一石塊放入量筒中水面上升10cm、總容積200cm³，未放入石塊前、水容積為150ml，則量筒底面積是
(A)1 (B)5 (C)10 (D)15 cm²。

【答案】：(B)

【解析】：石塊的體積＝水面上升的體積＝量筒底面積×液體上升高度，假設底面積為A
200－150＝50cm³ ＝A×10 A ＝ 5 cm²

( )30. 某人撿到奇形怪狀的石頭，該以何種方法測量其體積最恰當？
(A)先將石頭熔化後以量筒測量其體積 (B)用彈簧秤秤出其重量，再代入密度的公式求得體積 (C)測量其最長及最短的直徑後，求平均值，再代入體積的公式 (D)把石頭投入盛有已知體積的水的量筒中，直接測量其水量的變化。

【答案】：(D)

【解析】：測量不規則物體的體積，將物體直接投入量筒中，直接測量投入前的體積與投入後的體積，兩者的體積變化，即為不規則物體的體積。
不規則物體的體積＝物體投入後液體上升的體積－物體投入前的液面體積。

( )31. 四位同學以直尺(最小刻度為0.1公分)測量課本長度，結果如下表，則哪些同學的表示法是正確的？
(A)小彬與錦松　(B)小彬與一忠　(C)秀秀與一忠　(D)錦松與秀秀。

【答案】：(C)

【解析】：最小刻度為0.1公分，則估即值為0.01公分，因此測量值需表示到公分以下第二位，
因此16.60公分與15.59公分，皆為正確的表示結果。
16(公分).6(0.1公分，最小刻度)0(0.01公分，估計值)
15(公分).5(0.1公分，最小刻度)9(0.01公分，估計值)

( )32. 下列哪一種形狀不規則的物體較適合使用排水法來測量體積？
(A)鐵釘　(B)保麗龍球　(C)食鹽　(D)方糖。

【答案】：(A)

【解析】：不規則的沉體，能以量筒直接測量水位的變化，因此鐵釘可用排水法。
保麗龍球會浮於水面，無法完全沉入，需用重錘法測量體積。
食鹽、方糖都會溶於水，無法直接投入水中測量體積。

( )33. 如圖，以直尺測量鐵釘長度，圖中的數字代表公分，則鐵釘的長度應記為多少公分？
(A)6.000公分　(B)6.00公分　(C)6.0公分　(D)6公分。

【答案】：(B)

【解析】：如圖，最小刻度為0.4公分，鐵釘長度為8－2＝6公分，
應表示成6.00公分。
6(公分).0(公釐，最小刻度)0(0.1公釐，估計值)

( )34. 小明的爸媽買了一間三房兩廳的新公寓，每一個房間的格局都非常方正，小明趁著還未裝潢時，拿起皮尺丈量自己的房間，地板的長、寬都是4.5公尺，試問小明的房間大約有幾坪呢？(1坪＝3.305平方公尺)
(A)3坪　(B)6坪　(C)9坪　(D)12坪。

【答案】：(B)

【解析】：長寬皆為4.5公尺，面積為4.5×4.5＝20.25 m²
20.25 m2÷3.305 ＝6.12坪 ≒ 6坪

( )35. 下列哪一項測量結果，不能算是完整的敘述？　(A)課本的寬度為3.4個鉛筆盒長　(B)心怡的的身高160　(C)凱心100公尺跑15.2秒　(D)這張圖的面積30平方公分。

【答案】：(B)

【解析】：測量值需包含數字與單位，才是完整的敘述，因此身高160缺少單位，不是完整的表示法。

( )36. 美華用最小刻度單位為公分的直尺來測量不同物體長度，以下何者測量結果較合理？
(A)自然與生活科技課本長21.85公分　(B)原子筆長14.4公分　(C)100張紙厚度1.05公分　(D)十元硬幣厚度為0.25公分。

【答案】：(B)

【解析】：最小刻度為公分，則倒數第二位的單位為公分，最後一位(估計值)為公釐
(A) 21(公分).8(公釐，最小刻度)5(0.1公釐，估計值)，最小刻度為公釐。
(B) 14(公分，最小刻度).4(公釐，估計值)，最小刻度為公分。
(C) 1(公分).0(公釐，最小刻度)5(0.1公釐，估計值)，最小刻度為公釐。
(D) 0.2(公釐，最小刻度)5(0.1公釐，估計值)，最小刻度為公釐。

( )37. 有一個長方體的積木，如圖，祐瑟量出長、寬、高分別為3、5、8公分，則圖中甲、乙、丙面積的大小關係應為何？
(A)丙＞乙＞甲　(B)乙＞丙＞甲　(C)甲＞丙＞乙　(D)丙＞甲＞乙。

【答案】：(A)

【解析】：面積：甲＝3×5＝15cm² 乙＝3×8＝24cm² 丙＝5×8＝40cm²
面積大小： 丙＞乙＞甲

( )38. 為測量一枝湯匙的體積，嘉璐先在量筒中倒入15.0毫升的水，當湯匙完全沒入水中後，量筒的水體積上升至17.5毫升，則這支湯匙的體積是多少？
(A)17.5　(B)15.0　(C)2.5　(D)5.0　立方公分。

【答案】：(C)

【解析】：湯匙體積＝17.5－15.0＝2.5毫升。

( )39. 琦琦用直尺量測一桌長記為0.550m，則她所用的直尺準確至哪一單位？
(A)m　(B)cm　(C)mm　(D)km。

【答案】：(B)

【解析】：0(公尺).5(公寸)5(公分，最小刻度)0(公釐，估計值)

( )40. 佳蓉想測量一個錫做的小騎兵的體積，他先將水倒入量筒中，至水面為100.0立方公分處，將騎兵投入並完全沒入水中時，發現水面上升至180.0立方公分處，試問此騎兵的體積為多少立方公分？
(A)80.0立方公分　(B)100.0立方公分　(C)180.0立方公分　(D)280.0立方公分。

【答案】：(A)

【解析】：錫製的小錫兵能完全沒入水中，以沉體法：
小錫兵的體積＝末水面－初水面 ＝ 180.0－100.0 ＝80.0立方公分

( )41. 在一量筒內預先投入一鐵球，再倒入水至水面刻度為100.0cm為止，然後又投入一銅球沒入水中，發現水面升至180.0cm的刻度線，若將鐵球和銅球都取出後，發現水面降至40.0cm之刻度線，則鐵球與銅球的體積各為何？
(A)鐵球＝60cm、銅球＝80cm　(B)鐵球＝60cm、銅球＝100cm　(C)鐵球＝80cm、銅球＝80cm　(D)鐵球＝100cm、銅球＝80cm。

【答案】：(A)

【解析】：最低水面為40.0cm³，最高水面(鐵球＋銅球)為180.0cm³，
投入鐵球時，水面上升至100.0cm³，
則鐵球體積 ＝ 100.0 － 40.0 ＝ 60.0cm³
銅球體積 ＝ 180.0 － 100.0 ＝ 80.0cm³

( )42. 甲、乙二生測同一物長，結果所獲得的數值分別為30.5、290。其原因可能為何？
甲.所用單位長不同； 乙.測量儀器最小刻度單位不同； 丙.測量方法不正確。
(A)僅甲　(B)僅甲乙　(C)僅丙　(D)甲乙丙皆可能。

【答案】：(D)

【解析】：30.5與290所得結果不同，可能是估計值不同，可能是測量的單位不同，也可能是測量方法不正確，以上皆有可能。

( )43. 小彤測量一個長方體的積木，量出長、寬、高分別為3、5、8公分，則此長方體的體積應該為多少立方公分？
(A)16立方公分　(B)79立方公分　(C)120立方公分　(D)158立方公分。

【答案】：(C)

【解析】：長方體的體積＝長×寬×高＝3×5×8＝120cm³

( )44. 明明用最小刻度為公釐的直尺測得手掌長度為17公分時，他應該如何記錄？
(A)17公分　(B)17.0公分　(C)17.00公分　(D)17.000公分。

【答案】：(C)

【解析】：最小刻度為公釐，應準確到公釐，估計到0.1公釐。
手掌長度17公分，應表示為17.00公分
17(公分).0(公釐，最小刻度)0(0.1公釐，估計值)

( )45. 阿醜和阿美兩人用同一枝直尺去量同一枝筆的長，則所得的測量結果將如何？
(A)接近，但可能因估計而有不同　(B)必完全相同　(C)必定相差很大　(D)無法比較。

【答案】：(A)

【解析】：用同一支尺，測量同一物體，尺的最小刻度相同，但因每個人的估計值不一定相同，因此若測量方法正確，所測得的結果應很接近，但是測量值不一定相同。

( )46. 量筒內裝有水100c.c.，今投入一軟木時，水位升至125c.c.，但軟木浮起，則軟木體積為何？
(A)小於25c.c.　(B)剛好25c.c.　(C)大於25c.c.　(D)無法判定。

【答案】：(C)

【解析】：水面上升的體積＝軟木下沉的體積＝125－100＝25cc，
因軟木無法完全沉入水中，因此軟木真正的體積，將比下沉的體積大，因此大於25cc。

( )47. 下列哪一項敘述無法清楚描繪出測量的結果？
(A)車子的長度為3.58公尺　(B)鉛筆的重量為17.50公克　(C)喬丹出手投籃的過程需要0.15秒　(D)心跳72。

【答案】：(D)

【解析】：心跳72缺少單位，無法完整地表示結果。

( )48. 育航使用直尺測量自然與生活科技課本的長度，試問下列哪一種方式無法增加測量的準確性？
(A)選擇刻度較小的直尺　(B)選擇長度較短的直尺　(C)測量時應小心謹慎　(D)多次測量求出平均值。

【答案】：(B)

【解析】：最小刻度愈小、多次測量再求得平均、測量時小心謹慎，皆可提高測量的準確值。
和測量儀器尺的長短無關。

( )49. 怡真想要測量桌子的高度，使用下列哪一種單位較恰當？
(A)公分　(B)公里　(C)公升　(D)毫升。

【答案】：(A)

【解析】：桌子的高度約數十公分，因此以公分表示較為恰當。

( )50. 用不同的視線角度讀取量筒中水的體積時，下列哪一項才是正確的觀察方式？
(A) (B) (C) (D)

【答案】：(C)

【解析】：觀察量筒的液面體積，視線須和量筒的刻度面垂直，且測量液面的中央最低點。

( )51. 佳伶在課堂上學到測量結果的數字部分是由一組準確值和一位估計值所組成，於是他用直尺測量一枝鉛筆的長度，將測量結果記為20.05公分，由此可知此直尺的最小刻度為何？
(A)0.05公分　(B)10公分　(C)0.1公分　(D)0.01公分。

【答案】：(C)

【解析】：20(公分).0(公釐，最小刻度)5(0.1公釐，估計值)
最小刻度為公釐(0.1公分)。

( )52. 有一個長方體的積木，小白量出長、寬、高分別為3、5、8公分，則此長方體的總表面積應該為多少平方公分？
(A)16平方公分　(B)79平方公分　(C)120平方公分　(D)158平方公分。

【答案】：(D)

【解析】：長方體的表面積 ＝ (長×寬＋高×寬＋高×長)×2 ＝ (3×5＋5×8＋3×8) ＝79×2＝158 cm²

( )53. 紹華使用直尺測量鐵釘長度，直尺與鐵釘的相關位置如圖，若圖中直尺的數字以公分為單位，則鐵釘的長度應記錄為多少公分？
(A)16.0公分　(B)16.00公分　(C)3.00公分　(D)3.0公分。

【答案】：(C)

【解析】：鐵釘長度為13到16公分，長度＝16－13＝3公分，
尺面的最小刻度為公釐，因此鐵釘長度需表示成3.00公分
3(公分).0(公釐，最小刻度)0(0.1公釐，估計值)

( )54. 湘雅以相同的直尺測量鉛筆的長度五次，將測量結果記錄如表，則該鉛筆的長度應記為多少公分？
(A)15.2公分　(B)15.3公分　(C)15.4公分　(D)15.5公分。

【答案】：(C)

【解析】：多次測量求平均，所得值＝(15.5＋15.3＋15.5＋15.4＋15.3) ÷ 5 ＝ 15.4 公分
或是 ( 0.5＋0.3＋0.5＋0.4＋0.3) ÷ 5 ＝ 2.0 ÷ 5 ＝ 0.4
15＋0.4 ＝ 15.4公分

( )55. 世華想利用排水法來測量石頭的體積，於是他先在量筒中倒入20.0毫升的水，當石頭完全沒入水中後，量筒中的水面上升至22.5毫升，則這顆石頭的體積為何？
(A)22.5毫升　(B)20.0毫升　(C)2.5毫升　(D)5.00毫升。

【答案】：(C)

【解析】：排水法量石頭體積 ＝ 22.5－20.0 ＝ 2.5cm³

( )56. 小銘、小華、小仁三人利用直尺測量大同寶寶的高度，測量結果為：小銘18.05公分、小華17.95公分、小仁18.00公分，則下列敘述何者正確？
(A)三人的平均值為18.00公分　(B)直尺的最小刻度單位為0.01公分　(C)小銘測量的準確數值為18　(D)小華測量的估計數值為17.9。

【答案】：(A)

【解析】：平均值＝(18.05＋17.95＋18.00) ÷ 3 ＝ 18.00公分
測量值含2位小數，最小刻度為0.1公分，估計值為0.01公分
小銘的準確值為18.0公分，估計值為0.05公分
小華的準確值為 17.9 公分，估計值為 0.05公分

( )57. 天仁用刻度單位為cm、最小刻度為1mm的直尺量一枝鉛筆的長度，將筆的一頭對齊尺上刻度0時，筆的另一頭在刻度17到18當中的第四格到第五格間，請估計這枝鉛筆的長度？
(A)17.4cm　(B)17.5cm　(C)17.41cm　(D)17.041cm。

【答案】：(C)

【解析】：最小刻度為公釐，則測量值應準確到公釐，估計到0.1公釐
筆的另一頭在刻度17到18當中的第四格到第五格間，估計為17.45公分
鉛筆長度 ＝ 17.45 － 0 ＝ 17.45公分
17(公分).4(公釐，最小刻度)5(0.1公釐，估計值)

( )58. 育誠測量家中院子的面積，他測得的數值為長20公尺，寬10公尺請問院子的面積應該是多少？(1坪＝3.3平方公尺)
(A)300平方公尺　(B)200平方公分　(C)660坪　(D)60.6坪。

【答案】：(D)

【解析】：院子面積＝20×10＝200平分公尺＝200÷3.3＝60.6坪

( )59. 以下何種固體不適合用排水法來測量體積？
(A)石頭　(B)砂糖　(C)鐵　(D)金。

【答案】：(B)

【解析】：排水法適合測量能沉入水中且不會溶於水的固體，因此砂糖會溶於水，不適合用排水法測量。

( )60. 欲測量一滴水的體積，採用下列哪一個方法最好？
(A)以有刻度的滴管吸取一滴水測之　(B)以滴管滴50滴水於15c.c.的量筒中，讀取量筒中水的體積再除以50　(C)將一滴水滴入量筒中直接讀取　(D)將一滴水直接滴於桌面，先求得圓面積再乘以擺一支尺於桌面所測得的高，即是一滴水的體積。

【答案】：(B)

【解析】：測量液滴水的體積，直接取一滴測量，誤差會太大，應以滴管吸取多量加入量筒中，如取50滴液體倒入量筒後，再求平均值，可得較正確的結果。

二、填充題：

1. 最小刻度為mm的尺，測得物體長恰1公尺5公釐，則應記作_____m或_____厘米。

【答案】：1.0050、 100.50

【解析】：最小刻度為mm，應準確到mm，估計到0.1mm
1(公尺)5公釐＝1.005公尺，考慮科學記號，應寫成1.0050公尺
1(公尺).0(公寸)0(公分)5(公釐，最小刻度)0(0.1公釐，估計值)
100(公分).5(公釐，最小刻度)0(0.1公釐，估計值)

2. 某生用最小刻度公釐的直尺，測得物體長正好是36公分時，則最好記為_____公尺，或_____公分，或_____公釐。

【答案】：0.3600、 36.00 、360.0

【解析】：最小刻度為公釐，應準確至公釐，估計至0.1公釐
36公分應表示成36.00公分＝360.0公釐＝0.360公尺
36(公分).0(公釐，最小刻度)0(0.1公釐，估計值)
360(公釐，最小刻度).0(0.1公釐，估計值)
0(公尺).3(公寸)6(公分)0(公釐，最小刻度)0(0.1公釐，估計值)

3. 甲生測得桌長為12.84cm，則所用尺的最小刻度為_______。

【答案】：mm(公釐)

【解析】：12.84cm最小刻度應為公釐，準確到公釐，估計到0.1公釐
12(公分).8(公釐，最小刻度)4(0.1公釐，估計值)

4. 某生以最小刻度為公釐的直尺，測得拾圓硬幣直徑為2.5公分，則應記為_____公分或______公釐或______公尺。

【答案】：2.50、 25.0、 0.0250

【解析】：最小刻度為公釐，則2.5公分 應表示成 2.50公分
2(公分).5(公釐，最小刻度)0(0.1公釐，估計值)
2.50公分＝25.0公釐＝0.0250公尺
25(公釐，最小刻度).0(0.1公釐，估計值)
0(公尺).0(公寸)2(公分)5(公釐，最小刻度)0(0.1公釐，估計值)

5. 小明從同一規格的鐵釘中，任意取出六支，以直尺測量其長度，結果記為60.1公釐、60.0公釐、60.2公釐、60.3公釐、60.0公釐、50.1公釐，試問：
(1) 小明所使用直尺的最小刻度是______。
(2) 該一規格鐵釘的平均長度為______公分。

【答案】：(1) mm、 (2) 6.01

【解析】：60.1公釐，最小刻度為公釐，估計至0.1公釐
60(公釐，最小刻度).1(0.1公釐，估計值)
平均值＝(60.1＋60.0＋60.2＋60.3＋60.0)÷5＝60.12mm＝60.12cm
考慮最小刻度，應表示為60.1公釐(將下一位四捨五入，求至估計值)
60(公釐，最小刻度).1(0.1公釐，估計值)2(多餘的位數，四捨五入，故捨去)

6. 牆上掛著溫度計，小孩去看溫度時，因為眼睛位置低，看到的溫度比實際溫度____些。
(設刻度在水銀柱的後面)。

【答案】：高

【解析】：刻度在水銀液面之後，小孩由低處向上看，先見液面再見刻度，所得的數值應較原有的測量值高。

7. 某生用直尺測量1000張紙總厚度，再求每張紙平均厚度為0.0123公分，則：
(1) 某生使用直尺的最小刻度為______。
(2) 若測此種紙張共200頁，則厚度應記為_______公分。

【答案】：(1) cm (2) 1.2

【解析】：(1)0.0123公分為1000張紙的平均值，原有的測量值應為0.0123cm×1000＝12.3cm
12.3cm，最小刻度應為cm
12(cm，最小刻度).3(mm，估計值)
(2) 200頁共有100張紙，每張紙的平均厚度為 0.0123cm×100＝1.23cm
考慮尺的最小刻度為cm，則應表示為 1.2cm
1(cm，最小刻度).2(mm，估計值)

8. 一段路長為4.1732×10⁶cm，則測量時所使用的最小刻度為________。

【答案】：公引

【解析】：4.1732×10⁶ cm，代表最小刻度的準確值數字為3，
4.173×10⁶cm＝4.173×10¹km＝41.73公里
41(公里).7(公引，最小刻度)3(公丈，估計值)

9. 某人測100張紙厚度，求得每張紙平均值為0.865mm，則此人使用直尺的最小刻度為______。

【答案】：mm

【解析】：0.865mm是計算所得的平均值，原有的測量值應為 0.865mm×100＝86.5mm
最小刻度應為mm
86(公釐，最小刻度).5(0.1公釐，估計值)

10. 某生測量一小包細砂體積，把乾燥砂放入量筒中，輕敲量筒後砂面刻度280cm³，則：

(1) 細砂的體積______280cm³。(填：大於、小於或等於)

(2) 另取一個量筒盛水250cm³倒入盛細砂的量筒內，結果水面的刻度為430cm³，倒250cm³的水，但砂面上的水只有150cm³這是因為__________________。

(3) 承上題，細沙真正體積應為_____cm³，細砂間空隙總體積應為______cm³。

(4) 本實驗是利用細砂的何種性質來測量其體積?__________________。

【答案】：(1) 小於 (2) 水滲入砂中空隙 (3) 180、100 (4) 砂不溶於水，且沉於水中

【解析】：(1) 砂面原有280cm³，其中包含砂粒與空隙，因此砂粒的體積應小於280cm³。
(2) 盛水250 cm³倒入後，水面上升至430cm³，砂面上的水有430－280＝150cm³，
此因水滲入砂中的空隙。
(3) 最高水面的體積＝水的體積＋砂的體積
430＝250＋V V＝430－250＝180cm³ 細沙體積＝180cm³
280＝180＋空隙 空隙＝280－180＝100cm³
(4) 以量筒測量細砂的體積，是利用砂不溶於水，，且沉於水中。

11. 最小刻度為0.1cm³的量筒測量某液體，如圖，則液體的體積為______cm³。

【答案】：7.20

【解析】：如圖，水面刻度為7.2cm³，最小刻度為0.1cm³，應表示為7.20cm³。

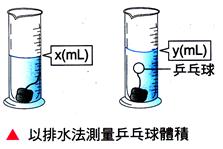
12. 有一量杯裝水35c.c，水面的刻度是7公分。今有甲、乙、丙三個學生欲度量一乒乓球之體積，每人的實驗步驟如下：

甲、 甲生將乒乓球置於量筒內，當乒乓球靜止時，測出水面刻度9公分；

乙、 乙生用手將乒乓球完全壓入水中，測出水面的刻度是12公分；

丙、 丙生將一石塊投入水中，測出水面的刻度是15公分，再將乒乓球下面繫該石塊，一起沒入水中，測出水面的刻度是19公分。
試回答下列各題：

(1) 由上面實驗步驟可知，______之實驗最正確。

(2) 量筒底面積______cm²；石塊體積______cm³；乒乓球體積______cm³。

【答案】：(1) 丙 (2) 5、40、20

【解析】：(1) 丙為重錘法，乒乓球會浮於水面，以重錘法測量，結果較為準確。
(2) 裝水35cc，，水面高度為7cm，底面積＝35÷7＝5cm²
石頭投入水中，水面上升15－7＝8cm，
石塊體積＝底面積×高＝5×8＝40cm³
乒乓球沉入水中後，水位由15cm上升至19cm，共上升4cm
乒乓球體積＝5×4＝20cm³

13. 使用一量筒，預先投入一鐵球，再倒入水至100.0cm³，的刻度線，然後又投入一銅球沒入水中，發現水面升至180.0cm³的刻度線，若將鐵球和銅球都取出後，水面降至40.0cm³之刻度線，則：

(1) 銅球的體積為______cm³；

(2) 鐵球的體積為______cm³。

【答案】：(1) 80.0 (2) 60.0

【解析】：最低水面體積為 40.0 cm³，最高水面體積為 180 cm³，只沉入鐵球時的體積為 100.0 cm³
鐵球體積 ＝ 100.0－40.0 ＝ 60.0 cm³
銅球體積 ＝ 180.0－100.0 ＝ 80.0 cm³

14. 小玉用40張方格紙，長、寬分別為60公分、30公分，質量共180公克；則：

(1) 每一平方公分的質量為_____公克。

(2) 若依比例尺的比例10⁴：1在方格紙上晝地圖，再將此地圖用剪刀剪下秤之為5.0公克，則此地圖所代表之面積為______平方公里。

【答案】：(1) 2.5×10^－3 (2) 20

【解析】：面積愈大，質量也愈大，面積比＝質量比
40張紙共180克， 每張紙質量＝180÷40＝4.5公克
一張紙面積60×30＝1800cm²，平均每1cm²質量＝4.5÷1800＝2.5×10^－3公克
比例尺＝1：10⁴＝1：10000，
地圖上1cm，實際長度為10000cm，即100公尺＝0.1公里
地圖上面積1cm²，實際面積為(0.1 km)²＝0.01 km²
1：2.5×10^－3＝A：5.0 A＝ 2000 cm²
1：0.01＝2000：X X＝20 km²

15. 某鄉鎮的地圖比例尺為1：5000，則：

(1) 有一處面積為200公畝的農地，在地圖上的面積為______cm²；

(2) 地圖上有一條河流寬度為1.5cm，則實際上此河流的寬度為______公尺；

(3) 有一處面積為5公頃的公園，在地圖上標示的面積為______cm²。
(1公頃＝100公畝；1公畝＝100平方公尺)

【答案】：(1) 8 (2) 75 (3) 20

【解析】：比例尺＝1：5000，表示：
地圖上1cm，實際長度為5000cm，即為50 m
地圖面積為1cm²，實際面積為 (50m)²＝2500 m²＝25公畝
(1) 面積 1：25＝A：200 A＝8 cm²
(2) 長度 1：50＝1.5：X X＝75 m
(3) 5公頃＝500公畝 1：25＝A：500 A＝20cm²

16. 一地圖繪製時的比例尺為1：1000000；則要將整個地圖面積覆蓋，共需要______張此種地圖。

【答案】：10¹²

【解析】：地圖長度：實際長度＝1：1000000＝1：10⁶，則：
實際面積上以地圖覆蓋，長需鋪10⁶張，寬需鋪10⁶張
共需 10⁶×10⁶＝10¹² 張

17. 若需10⁸張臺灣省地圖才能完全覆蓋臺灣省土地，則臺灣省地圖與臺灣省土地比例尺為______。

【答案】：1：10000

【解析】：以地圖覆蓋，需10⁸張，表示： 實際面積是地圖面積的10⁸倍
地圖面積：實際面積＝1：10⁸＝1²：(10⁴)²
地圖長度：實際長度＝1：10⁴＝1：10000

18. 某土地的實際面積為2.5×10² m²，但在地圖上的面積則僅有2.5 cm²，則地圖與實際地形繪製時的比例尺為______。

【答案】：1：1000

【解析】：地圖面積：實際面積＝2.5cm²：2.5×10²m²＝2.5cm²：2.5×10⁶cm²＝1：10⁶＝1²：(10³)²
地圖長度：實際長度＝1：10³ ＝1：1000

19. 某塊土地與其地圖的比例尺為2000：1，則需______張地圖可將土地完全覆蓋。

【答案】：4×10⁶

【解析】：地圖長度：實際長度＝1：2000，表示： 實際長度為地圖長度的2000倍
實際面積上以地圖覆蓋，長需鋪2000張，寬需鋪2000張
共需 2000×2000＝4×10⁶ 張

20. 下列各項體積：(A)1公秉 (B)100公升 (C)10立方公尺 (D)10⁷c.c；以上各項體積由大至小依次為_____________。(填代號)

【答案】：(C)＝(D)＞(A)＞(B)

【解析】：1公秉＝1m³＝1000公升
10m³＝10×10³公升＝10×10⁶cc＝10⁷ cc
10m³＞1公秉＞100公升
10 m³＝10⁷ cc＞1公秉＞100公升
C＝D＞A＞B

21. 某地圖的比例尺為1：10000，則：

(1) 地圖上25 cm的長度，實際上_____公尺，相當於______公里；

(2) 地圖上25 cm²的面積，實際上為______m²，相當於______km²；

(3) 某公路的實際長度為5 km，地圖上的長度應為_______公分；

(4) 某菜園的實際面積為2.5×10⁴ m²，在地圖上的面積應為_______cm²。

【答案】：(1) 2500、2.5 (2) 2.5×10⁵、0.25 (3) 50 (4) 2.5

【解析】：比例尺1：10000 地圖上1 cm，實際長度為10000cm，即100 m
(1) 1：100＝25：X X＝2500公尺＝2.5公里
地圖上1cm，實際長度為100m，則：
地圖上1cm²，實際面積為100×100＝10⁴ m²
(2) 1：10⁴＝25：X X＝25×10⁴m²＝2.5×10⁵m²＝2.5×10^－1km²＝0.25km²
(3) 1：100＝Y：5000 Y＝50
(4) 1：10⁴＝Y：2.5×10⁴ Y＝2.5 cm²

22. 長15公尺、寬10公尺、深1.6公尺的游泳池，將水裝滿，最多可盛水_____立方公尺，相當於_______公升＝_______公秉＝_______毫升＝_______公撮＝_______c.c。

【答案】：240、2.4×10⁵、240、2.4×10⁸、2.4×10⁸、2.4×10⁸

【解析】：1公秉＝1m³＝10³公升
15m × 10m × 1.6m ＝ 240m³ ＝ 240公秉 ＝ 2.4×10²公秉＝2.4×10⁵公升
＝ 2.4×10⁸毫升＝2.4×10⁸公撮＝2.4×10⁸cc

23. 大小兩量筒底面半徑比為2：1，今將定量的水倒入小量筒中，水面上升10cm，則：

(1) 將等量的水倒入大量筒中，水面將升高_______cm；

(2) 若小量筒的半徑為5cm，則量筒中的水量為_______毫升；

【答案】：(1) 2.5 (2) 785

【解析】：底面辦競比為2：1，，底面積比為4：1，
大量筒的底面積為4，小量筒的底面積為1
小量筒內液體的體積＝大量筒內液體的體積
4×h＝1×10 h＝2.5cm
小量筒的半徑為5cm時，(3.14×5×5)×10＝785 cm³＝785毫升

24. 某圓柱形容器容積為450 cm³，裝300 cm³水後，發現液面的高度為10公分，則：

(1) 此容器的底面積為_______平方公分；

(2) 放入木塊後溢出60c.c，且木塊露出70cm³於水面上，則木塊體積_______cm³。

【答案】：(1) 30 (2) 280

【解析】：盛300cm³後的水位高度為10cm，則
底面積＝A×10＝300 A＝30 cm²
木塊的體積＝液體上升的體積＋液體溢出的體積＋露出液面的木塊體積
＝(450－300)＋60＋70＝150＋60＋70＝280cm³

25. 木塊和鐵塊共同放入裝有水的量筒中，水位為150cm³，如將鐵塊單獨放入量筒中，水位為130cm³，則木塊的體積為_______cm³。

【答案】：20

【解析】：木塊＋鐵塊石的水位＝150cm³，只沉入鐵塊石的水位＝130cm³
利用重錘法，求得木塊體積＝150－130＝20cm³

26. 使用一量筒，預先投入一鐵球，再倒入水至160.0 cm³，的刻度線，然後又投入一銅球沒入水中，發現水面升至250.0 cm³的刻度線，若將鐵球和銅球都取出後，水面降至90.0 cm³之刻度線，則：

(1) 銅球的體積為______cm³；

(2) 鐵球的體積為______cm³。

【答案】：(1) 90.0 (2) 70.0

【解析】：最低水面體積為 90.0 cm³，最高水面體積為 250 cm³，只沉入鐵球時的體積為 160.0 cm³
鐵球體積 ＝ 160.0－90.0 ＝ 70.0 cm³
銅球體積 ＝ 250.0－160.0 ＝ 90.0cm³

27. 將石塊投入盛有150 cm³水的量筒中，若水面上升10公分，且水位亦上升至200 cm³，則量筒底面積為_______cm²。

【答案】：5

【解析】：石頭體積＝水面升高體積＝底面積×高，假設底面積為A
200－150＝A×10 50＝A×10 A＝5 cm²

28. 有大小兩量筒，底面直徑比為4：1，今將一定量的水倒入小量筒中，若水深為48 cm，改倒入大量筒中時，水面的高度應為_______cm。

【答案】：3

【解析】：量筒直徑比為4：1，半徑比＝4：1，底面積比＝16：1
假設大量筒底面積＝16，則小量筒底面積＝1，
大量筒內液體體積＝小量筒內液體體積
16×h＝1×48 è 48÷16＝3 cm

排水法：	重錘法：
(1) 適合測量沉沒於水中的體積。 (2) 水面升高的體積 ＝ 石塊沒入水中的體積 ＝ 末體積－初體積 ＝ b－a (3) 沉體法和液體重類無關。	(1) 適合測量密度小，會浮於水面的物體體積。 (2) 在浮體(乒乓球)下方綁一重錘(鐵塊)，使重錘和浮體皆沉入水中。 (3) 鐵塊沉入後的體積至全部沉默的體積變化，才是乒乓球的真正體積 ＝y － x