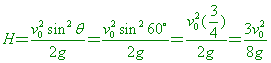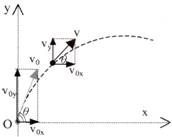
(一) 拋體分析：

A、 起始條件：

(1) 初速V₀，斜角θ
水平初速V_0x＝V₀cosθ(")
鉛直初速V_0y＝V₀sinθ(#)

(2) 受力情形：
水平方向不受力 [ 等速度運動(慣性定律)
鉛直方向受重力 [ 等加速度運動(運動定律)
V_0y向上，加速度a_y＝重力加速度＝g($) [ 鉛直上拋

B、 t秒後情形：

(1) 軌跡方程式：
x＝V_0x•t＝(V₀cosθ)•t [
[
[
[ 圖形為開口向下的拋物線 (y＝ax－bx²)

(2) V_x＝V_0x＝ V₀cosθ(")
V_y＝V_0y－gt＝V₀ sinθ－gt
[
[
速度方向即為物體運動的方向 θ：和水平面的夾角

C、 最高點：

(1) 時間(t)：
V_y＝0 [ V₀ sinθ－gt＝0 [

(2) 最大高度(H)：
最高點末速＝0 [
[ [

(3) 全程時間(T)：
a. 全程飛行時間＝最大點時間的2倍 [
b. 鉛直上拋過程，同一水平面(高度)的速度大小會相等，方向相反。
[ 鉛直初速＝V₀sinθ [ 鉛直末速＝－V₀sinθ
－V₀sinθ＝V₀sinθ－gT [ 2V₀sinθ＝gT [

(4) 水平射程(R)：
[

(5)

[ 或 R＝4Hcotθ

D、 切線加速度(a_t)與法線加速度(a_n)：
[ a_t＝gsinθ a_n＝gcosθ
最高點處 V_y＝0 V_x＝V₀ cosθ [ a_t＝0 a_n＝g($)

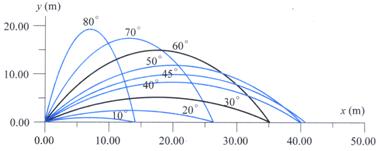
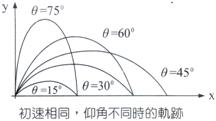
(二) 討論：

A、 最大水平射程：
為最大值時 [ sin2θ＝1
此時 2θ＝90∘ [ θ＝45∘
當斜拋仰角為45∘時，有最大的水平射程R
[ 。
由圖形可發現：
當V₀維持一定時，將θ由0∘起逐漸增大，則水平射程亦逐漸增加，直到45∘時，水平射程達到最大值，超過45∘後增加θ值，則水平射程又逐漸減小。

B、 斜拋仰角互餘時：

(1) θ₁＋θ₂＝90∘ [ θ₂＝90∘－θ₁

當兩次的斜拋仰角互餘時，兩次的水平射程會相等。

(2) R₁＝R₂時 [ [ sin2θ₁＝sin2θ₂
sin2θ₁＝sin(180－2θ₁)＝sin2θ₂ [ 180－2θ₁＝2θ₂
[ 2θ₁＋2θ₂＝180∘ [ θ₁＋θ₂＝90∘
當兩次的水平射程相等時，斜拋的仰角必定互餘。

(三) 斜向拋射的特性：

A、 斜拋至最高點所需的時間t₁＝從最高點落回原高度所需的時間t₂。

B、 上升過程與下降過程中，在同一高度處有相同的速率，且角度相同，但是上升時原為仰角，下降至同一高度變為俯角。
水平等速度 [ V_1x＝V_2x＝Vcosθ
鉛直等加速度 [ V_1y＝V₁sinθ(#)
V₂y＝V₂sinθ($)
[

C、 上升與下降經相同的高度差，則所需的時間相同。
如上圖，A"P所經的時間，與P'"A'所經的時間相同。 [ t_AP＝t_P'A'。

D、 即使初速不同，飛行仰角不同，若鉛直速相同時，則：

(1) 飛行時間必定相同。

(2) 最大飛行高度必定相同。

1. 一物體自地面以20 m／s、30°的仰角被拋出，假設g＝10 m／s²，則：
(1)軌跡方程式【】；
(2)最大高度【5】m；
(3)飛行時間【2】s；
(4)水平射程【】m；
(5)落地時之切線加速度【5】m／s²；
(6)落地時之法線加速度【】m／s²。

【解析】：

(1) [

(2) [ [ H＝5m

(3) 飛行時間 [ －V_y＝V_y－gT [ －10＝10－10xT [ t＝2秒

(4)

(5) 拋出瞬間的仰角30∘，落地瞬間的俯角為30∘，
切線加速度a_t＝gsin30∘＝10x(1／2)＝5 m／s²

(6) 法線加速度

2. 一物斜向上拋，水平射程和最大高度相等，設拋射角和地面成θ角，則　
(A) tanθ＝4　(B) tanθ＝2　(C) cotθ＝4　(D) cotθ＝2

【答案】：(A)

【解析】： [
[ 4cosθ＝sinθ [ tanθ＝4

3. 某女同學進行跳遠測驗，在加速起跑後，以仰角37°從起跳線躍出，跳遠成績為4.8公尺，則此女同學從起線躍出時速度為　
(A) 6.3　(B) 6.8　(C) 7.1　(D) 7.5　m／s（g＝10 m／s²）

【答案】：(C)

【解析】： [
[ ＝7.05 m/s

4. 某女同學進行跳遠測驗，在加速起跑後，以仰角37°從起跳線躍出，跳遠成績為4.8公尺，若此同學再加速助跑，使躍出時的初速度增加20％，則跳遠成績可增加　
(A) 21％　(B) 30％　(C) 44％　(D) 50％

【答案】：(C)

【解析】：承上題，初速原為7.05 m/s，再增加20％，初速增為7.05x1.2＝8.46 m/s
最大水平射程
原有的水平設成為4.8m，因此增加了

5. 不計空氣阻力，某物體在水平面上斜拋，則上升過程中，最後一秒爬升的鉛直高度為若干？　
(A) 0.25g　(B) 0.5g　(C) g　(D) 1.25g　(E)條件不足（重力速度為g）

【答案】：(B)

【解析】：上升過程最後1秒的位移會等於從最高點開始落下第1秒內的位移

落下的第1秒位移5m，所以同一時間內上升的最後一秒位移＝5m＝0.5g。

6. 以v₀之初速斜向拋出一球，於運動過程中，速度最小值，則此球可上升的最大高度為　
(A)　(B)　(C)　(D)　(E)

【答案】：(D)

【解析】：最高點的速度為最小值，只有水平速度，
所以 [ [ θ＝60∘

7. 將一石子斜向拋射，不計空氣阻力時，在最高點之速率為拋出時速率之一半，則拋射角為　
(A) 30°　(B) 37°　(C) 45°　(D) 53°　(E) 60°

【答案】：(E)

【解析】：最高點的速度只有水平速度 [ [ [ θ＝60∘

8. 如圖，大砲以37∘瞄準前方400 m的峭壁射擊，已知砲彈初速100 m／s，砲彈發射後幾秒鐘擊中峭壁？　（cos37°＝0.8）　
(A) 5　(B) 10　(C) 15　(D) 20

【答案】：(A)

【解析】：砲彈的水平速度V_x＝V₀ cos37∘＝100x(4／5)＝80m/s
鉛直速度V_y＝V₀ sin37∘＝100(3／5)＝60 m/s
x＝V_xt [ 400＝80T [ T＝5秒

9. 一物體自地面被斜拋出去，如欲使水平射程R為最大高度H的3倍，則拋射時的仰角該為　
(A) 60°　(B) 53°　(C) 45°　(D) 37°　(E) 30°

【答案】：(B)

【解析】：R＝3H [ [
[ [ θ＝53∘

10. 一砲在高65公尺之崖邊，向海面射擊，初速為20公尺，仰角37°，恰可擊中停泊於海面的艦艇，則(g＝10 m／s²)
(1) 砲彈發射至擊中艦艇需【5】秒。
(2) 艦艇與砲的水平距離為【80】公尺。

【答案】：(C)

【解析】：
落於海面上，鉛直位移＝－65公尺 [
5t²－12t－65＝0 (5t＋13)(t－5)＝0 [ t＝5秒
水平位移R＝V_xt＝16x5＝80公尺

11. 以一定之初速，作兩次斜向拋射，其最大高度分別為 H₁ 及 H₂，若兩次水平射程相等，則此射程為【】。

【解析】： ，兩次水平射程相等 [
[ [
[

12. 一球自地表以v₀之初速、60˚之仰角斜向拋出，若不計空氣阻力，當球的速度與水平成30˚角之瞬間，球離地面的高度應為　
(A) 　(B) 　(C) 　(D) 　(E)

【答案】：(C)

【解析】： 水平初速
當速度的仰角變為30˚時，速度變為V₁，則
水平速度維持不變 [ [
鉛直初速

[ [

13. 如圖，自60 m高的樓頂以25 m／s的初速，仰角53°拋出一球，經幾秒後著地？
(A) 6　(B) 7　(C) 3　(D) 5　(重力加速度g＝10 m／s²)

【答案】：(A)

【解析】： m/s
m/s

落地位移＝－60m [
[ 5t²－20t－60＝0 (t－6)(t＋2)＝0 [ t＝6秒

14. 在高40 m處以20 m／s斜角30° 拋出一石，g＝10 m／s ²，則
(1)【4】秒著地。
(2) 2秒末之高度為【40m】，速度為【20 m/s】。
(3) 3秒末之高度為【25m】，速度大小為【m/s】。
(4)著地之速度為【】。

【解析】： m/s
m/s
(1) 落地位移＝－40m [ [ 5t²－10t－40＝0
t²－2t－8＝0 [ (t－4)(t＋2)＝0 [ t＝4秒
(2) 2秒末高度h₁
出發點距地面40m，2秒後位移為0，依然距離地面40m。
速度V_y＝v₀－gt＝10－10x2＝－10m/s，速度大小為10m/s，方向朝下。
V_x＝ m/s ，m/s
(3)3秒末高度h₁
出發點距地面40m，3秒後位移為－15m，因此距離地面40－15＝25m。
速度V_y＝v₀－gt＝10－10x3＝－20m/s，速度大小為20m/s，方向朝下。
V_x＝ m/s ， m/s
(4)著地瞬間的位移＝－40m [
[ 5t²－10t－40＝0 t²－2t－8＝0 (t－4)(t＋2)＝0
t＝4秒 [ V_y＝v₀－gt＝10－10x4＝－30m/s
V_x＝ m/s ， m/s

15. 自高度h的樓頂同時拋出兩球，速率均為v₀，方向分別是仰角45°及俯角45°，則兩球著地的水平位置相距多遠？
(A) 　(B) 　(C) 　(D) 。

【答案】：(B)

【解析】：如圖，仰角45∘，水平位移為AB'，
俯角45∘十，水平位移為A'B'，
由圖形知，A'B'＝AB，因此兩者的位移相差
＝AB'－A'B'＝AB'－AB＝B'B＝PP'＝

16. 以初速 v 仰角θ斜向拋出一球，空氣阻力不計，當球速度與水平夾角α時(α<θ)的速率為
(A) (B) (C) (D) (E) 。

【答案】：(A)

【解析】：拋射過程的任何位置，水平速度必定相等
[ V₁cosθ＝V₂cosα [

17. 一物體在平坦地面上以 15 m/s初速，37° 仰角拋出，則其水平射程為【21.6 m】。

【解析】：

18. 由地面向斜上方拋出質量m的物體，此物在達到最大高度h時仍有v的速率，則此物體初拋的速度為【】。

【解析】：最大高度h時，鉛直的初速為 [
拋射過程的水平速度為定值，始終都是v [ V_x＝v
[

19. 某物自地面作斜向拋射，其水平射程為頂點高度的4倍，則其拋射仰角為若干？
(A) 30°　(B) 37°　(C) 45°　(D) 53°　(D) 60°。

【答案】：(C)

【解析】：R＝4H [ [ sin2θ＝2sin²θ
[ 2sinθcosθ＝2sin²θ [ cosθ＝sinθ
[ tanθ＝1 [ θ＝45∘

20. 二拋體A、B的初速量值相等，其仰角分別為30°與60°自同一地點同時拋出，則：

(1) A、B二拋體水平射程比值為【1：1】。

(2) B二拋體最大高度比值為【1：3】。

【解析】：

21. 將一質點自地面斜向拋射出，最大高度為45公尺，期間有二個時刻質點位在25公尺高度，則此二個時刻分別為拋出後第【1】秒與第【5】秒。(g＝10 m／s²)

【解析】：最大高度＝45m [ 鉛直初速V_y²＝2gh＝2x10x45＝900 V_y＝30m/s
y＝25m [ [
5t²－30t＋25＝0 t²－6t＋5＝0 (t－1)(t－5)＝0 t＝1秒 或 t＝5秒

22. 不計空氣阻力，某物體在水平地面上作斜拋，已知飛行時間為 6 秒，則落地前 1 秒內落下的距離為【25 m】。(重力加速度為 g )

【解析】：全程為6秒 [ 到達最大高度需時3秒，落下需時3秒
落地前1秒距離＝落下3秒內距離－落下2秒內距離
＝ m

23. 某物在地表附近作斜拋，拋出後2秒末掠過大樓角落，如圖，再經3秒落地，若g = 10 m/s²，則大樓高度為【30 】公尺。

【解析】：全程時間＝2秒＋3秒＝5秒
到達最高點需費時＝5÷2＝2.5秒
則 鉛直初速：
第2秒末掠過大樓角落 [ 垂直高度

24. 一砲彈以仰角30°，初速400公尺／秒射出，若砲身高度及各種摩擦力都不計，砲彈飛行的時間(射出至落地)為【40秒】。

【解析】：V_y＝400sin30∘＝400x0.5＝200 m/s [ 落地瞬間鉛直速度＝－200m/s
－200＝200－10t [ t＝40秒